Binary search trees
A binary search tree is a binary tree where the left subtree has smaller elements and the right subtree has larger elements.
You can find the complete code for this and other data structures here: data structures and algorithms
What is a tree anyway
A tree is an undirected graph that satisfies any of the following definitions:
- Acyclic connected graph.
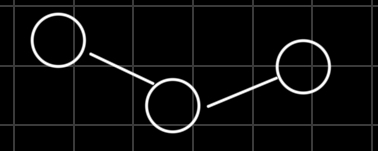
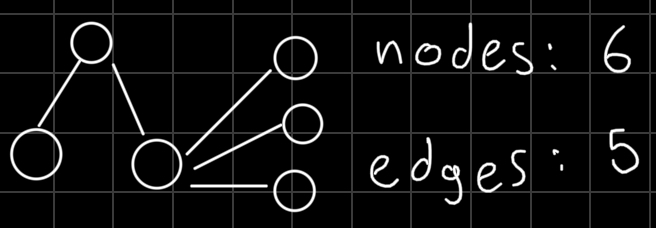
- Connected graph with N nodes and N-1 edges.
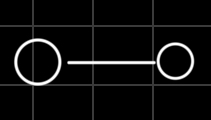
- 2 vertices 1 path (A graph in which any 2 vertices are connected by just one path).
Stuff we have to know
-
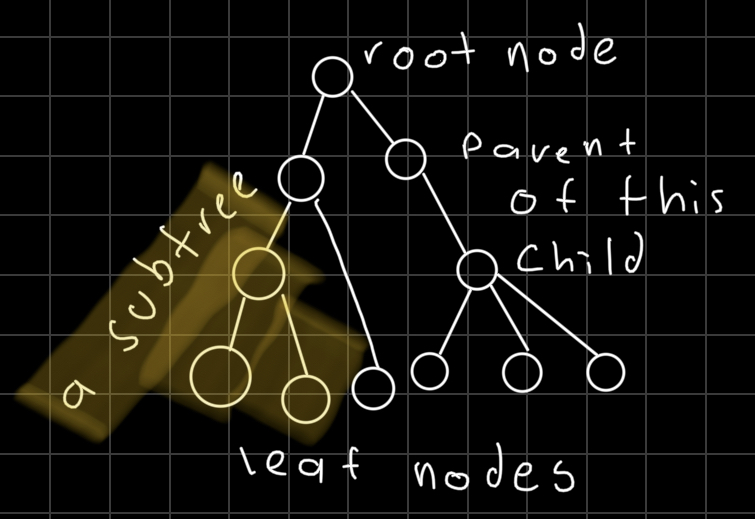
Rooted tree: Theres a root node and we hold a reference to it, we can choose any node as the root node.
-
Root node: It has no parent, but sometimes is useful to say that the parent of the root node is itself.
-
Child: Node that extends from another node, a Parent is the inverse of this.
-
Leaf node: Node with no children.
-
Subtree: Tree contained in another tree.
-
Binary tree: Every node has at most 2 children.
-
Binary search tree: Satisfies the BST invariant, left subtree has smaller elements and right subtree has larger elements.
Complexity of common operations
| Operation | Average | Worst |
|---|---|---|
| insert(element) | O(log(n)) | O(n) |
| remove(element) | O(log(n)) | O(n) |
| search(element) | O(log(n)) | O(n) |
Implementation
Binary Tree Node
This is what the class that we will be using as node looks like (setters and getters omitted).
class BinaryNode<T extends Comparable<? super T>> {
private BinaryNode<T> leftChild;
private BinaryNode<T> rightChild;
private T data;
public BinaryNode(T data) {
this.data = data;
}Insertion
A common theme is that we are going to have a public method and a private method.
If rootNode is null then it means that the tree is empty and we just set that new value as the root node of the tree.
If the root node already exists we call our private insertion method.
public boolean insert(T data) {
if(rootNode == null) {
rootNode = new BinaryNode<>(data);
length++;
return true;
}
return insert(new BinaryNode<T>(data), rootNode);
}Here we make sure to comply with the BST invariant and traverse the tree accordingly, smaller elements on the left, larger elements on the right.
If we find a leaf node then we set the new node as the child, incrementing the length of the tree and returning true to signify that the insertion was successful.
This implementation of the BST wont allow for duplicates, if we find one we return false.
private boolean insert(BinaryNode<T> newNode, BinaryNode<T> node) {
if(newNode.getData().compareTo(node.getData()) < 0) {
if(node.getLeftChild() == null) {
node.setLeftChild(newNode);
length ++;
return true;
}
return insert(newNode, node.getLeftChild());
}
if(newNode.getData().compareTo(node.getData()) > 0) {
if(node.getRightChild() == null) {
node.setRightChild(newNode);
length ++;
return true;
}
return insert(newNode, node.getRightChild());
}
return false;
}Contains
This method will let us know if a value is present in our BST, we have a public method that receives the value to look for:
public boolean contains(T data){
return contains(data, rootNode);
}And we have a private method that goes inside the tree looking for the value.
private boolean contains(T data, BinaryNode<T> node) {
if(node == null) {
return false;
}
if(data.compareTo(node.getData()) < 0) {
return contains(data, node.getLeftChild());
}
if(data.compareTo(node.getData()) > 0) {
return contains(data, node.getRightChild());
}
return true;
}Removal
In the public version of remove we receive the value to remove, we save the current size of the tree and then we call the recursive private version, if the new size is different then it means the value was removed.
public boolean remove(T data) {
int originalLength = length;
rootNode = remove(data, rootNode);
return originalLength != length;
}The recursive removal is very interesting, as we traverse the tree the recursive method also returns the correct child for the parent node. For example if we are going inside the right sub tree we do:
node.setRightChild(remove(data, node.getRightChild()));If we never find the value we want to remove we are just re-setting the children of the nodes we are traversing, but if we find a match we need to account for three cases.
- The node we want to remove is a leaf node.
- Has only a left or right child.
- Has both children.
For the first two cases we just return the opposite child, for example this is the case where the left child is null:
if(node.getLeftChild() == null) {
BinaryNode<T> rightChild = node.getRightChild();
node.setData(null);
node = null;
length--;
return rightChild;
}This also handles the case where we have a leaf node, for a node with a right child we would return the left child.
The last case, where a node has both children is tricky since we have to find a node that complies with the BST invariant.
There are two ways to ensure we comply with the BST invariant we can either find the leftmost child of the right node or the rightmost of the left node. In this implementation we go for the leftmost node of the right child using the following method:
private BinaryNode<T> getLeftmost(BinaryNode<T> node) {
while(node.getLeftChild() != null) {
node = node.getLeftChild();
}
return node;
}After that we copy the value to the node we are removing and then go inside the subtree in order to delete the node, since its the leftmost node we know that is going to fall in the case of a removal of a leaf node.
BinaryNode<T> tmp = getLeftmost(node.getRightChild());
node.setData(tmp.getData());
node.setRightChild(remove(tmp.getData(), node.getRightChild()));This is the complete code for the remove method.
private BinaryNode<T> remove(T data, BinaryNode<T> node) {
if(node == null) {
return null;
}
if(data.compareTo(node.getData()) < 0) {
node.setLeftChild(remove(data, node.getLeftChild()));
} else if(data.compareTo(node.getData()) > 0) {
node.setRightChild(remove(data, node.getRightChild()));
} else {
if(node.getLeftChild() == null) {
BinaryNode<T> rightChild = node.getRightChild();
node.setData(null);
node = null;
length--;
return rightChild;
}
if(node.getRightChild() == null) {
BinaryNode<T> leftChild = node.getLeftChild();
node.setData(null);
node = null;
length--;
return leftChild;
}
BinaryNode<T> tmp = getLeftmost(node.getRightChild());
node.setData(tmp.getData());
node.setRightChild(remove(tmp.getData(), node.getRightChild()));
}
return node;
}Download the complete code for this and other data structures here: data structures and algorithms.