Priority queue using binary heap
A priority queue is an abstract data type that saves items with a priority and when we fetch the next element (poll) we receive the element with the highest priority in the case of a max priority queue or the lowest priority if we are using a min priority queue.
You can find the complete code for this and other data structures here: data structures and algorithms
Common Operations for a priority queue includes:
| Operation | Complexity |
|---|---|
| poll() | O(log(n)) |
| add(element) | O(log(n)) |
One of the most common implementations of priority queue is by using a binary heap data structure because it provides all the functionality we need.
A heap is a tree data structure that satisfies the heap invariant and a binary heap means that every node on the tree can have at most two children.
- heap invariant: If A is a parent node of B then A is ordered with respect to B for all nodes A, B in the heap. In other words each parent node must be ordered in respect of its children.
We will use an array to represent the tree like this:
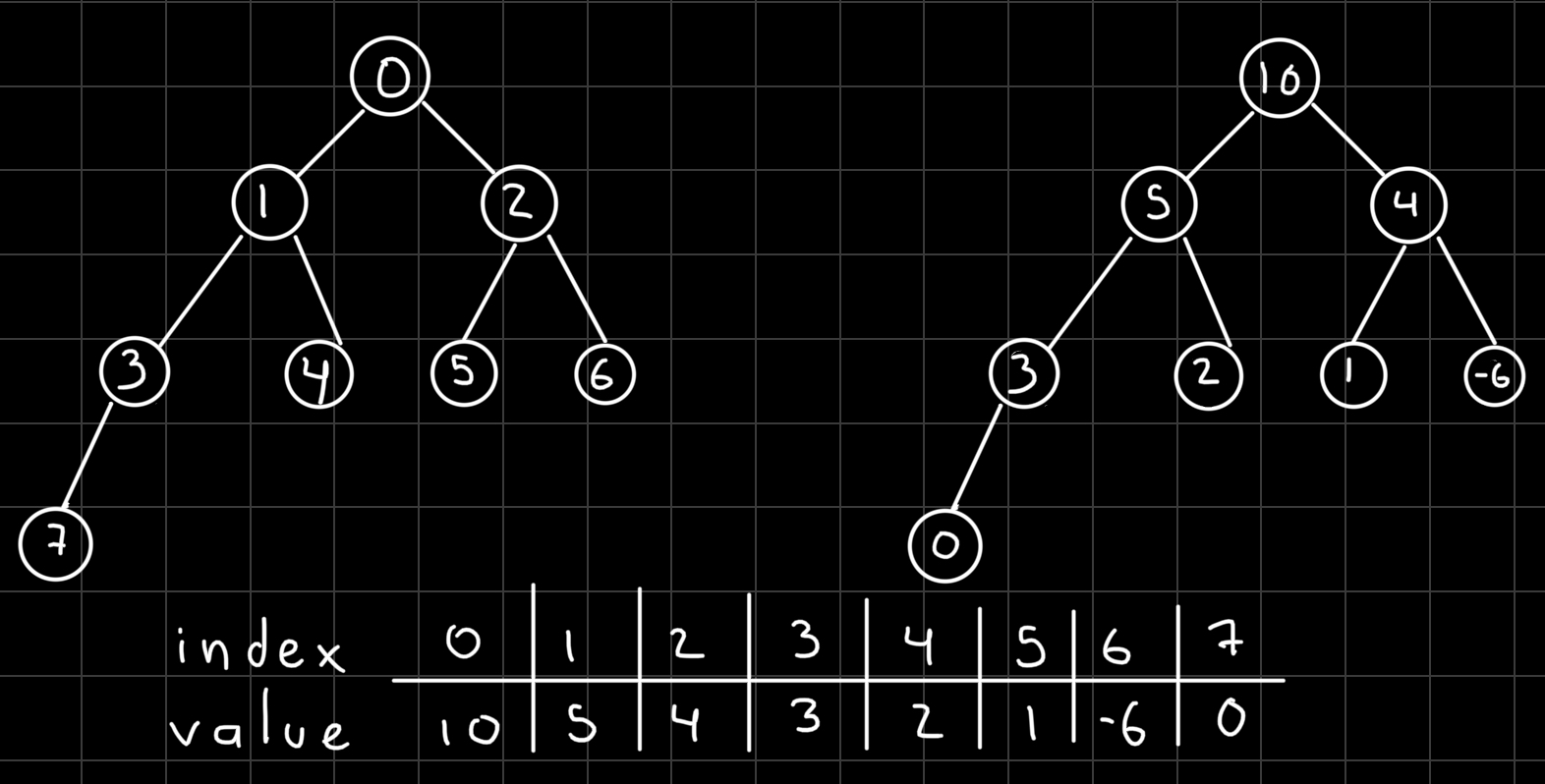
In the left tree you can see the index of the array and on the right one the priorities. This array represents a max binary heap. We always need to have a complete (or full) binary tree, this means that every level except possibly the last one is completely filled and all nodes are as far to the left as possible.
Now we need a way to get the left and right child from a parent and the parent from a child:
public int getLeftChild(int index) {
return 2 * index + 1;
}
public int getRightChild(int index) {
return 2 * index + 2;
}
public int getParent(int index) {
return (index - 1) / 2;
}In this implementation we will be able to pick if we are going to have a max or min priority queue at the moment of creation, for this we will have a property called max, if max is true then is a max priority queue and if max is false then is a min priority queue.
We will also only accept objects that implement the Comparable interface, and we will use the following method on the priority queue to compare two objects.
public int compare(int childIndex, int parentIndex) {
return array.get(childIndex).compareTo(array.get(parentIndex)) * (max ? 1 : -1);
}If max is false then we multiply by -1 the result of the compareTo method reversing the order.
To be able to bubble up a node we use a method that will recursively compare a child to its parent and swap them if needed and then repeat until the heap invariant is achieved.
public void siftUp(int index) {
if(index > 0 && compare(index, getParent(index)) > 0) {
swap(index, getParent(index));
siftUp(getParent(index));
}
}And then we also need to have a method to bubble down a node until the heap invariant is preserved. First we get both children of the node we want to bubble down and then check if we need to swap with one of the children, repeating recursively if needed.
public void siftDown(int parent) {
int current = parent;
int leftChild = getLeftChild(parent);
int rightChild = getRightChild(parent);
if(leftChild < array.size() && compare(leftChild, parent) > 0) {
current = leftChild;
}
if(rightChild < array.size() && compare(rightChild, current) > 0) {
current = rightChild;
}
if(parent != current) {
swap(parent, current);
siftDown(current);
}
}Finally in order to add an element to the priority queue, we put the new element at the end of the array and then we sift it up (bubble up).
public void add(T value) {
array.add(value);
siftUp(array.size() - 1);
}In the poll method we will first swap the 0 element with the last element, we remove it from the inner array and then we sift down the element at 0.
public T poll() {
T value = array.get(0);
swap(0, array.size() - 1);
array.remove(array.size() - 1);
siftDown(0);
return value;
}Download the complete code for this and other data structures here: data structures and algorithms.