N-Queens brute force
The N-Queens problem consists in finding a position for N chess queens in a board of NxN squares where none of the queens are attacking each other.
You can find the complete code for this post here: NQueensBruteForce.java.
In case you’re not familiar with the queens movement, the queen can move in every direction, across the column, row and diagonal that crosses the square where the queen is standing, we say that the queen is attacking those squares.
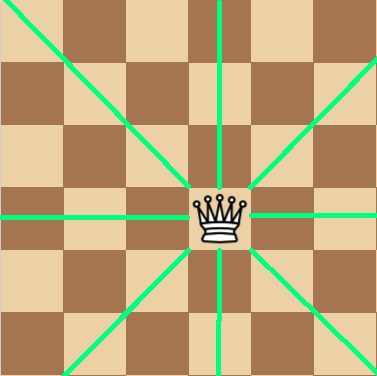
So a solution for the problem of N-Queens where N = 4 looks like this:
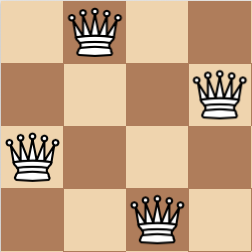
Since the queen attacks all the squares in the column there can be only one queen in each column and its the same for the rows, this gives us the possibility of representing a position using an array of length n. For the position above the array would be {1, 3, 0, 2}. Where every index in the array represents a column, and the value of that position in the array represents the number of the row (from 0 to N - 1).
For the brute force approach we need two things:
- a list of every possible
permutationof 0 to N - 1 - a way to check if that permutation is a solution or not.
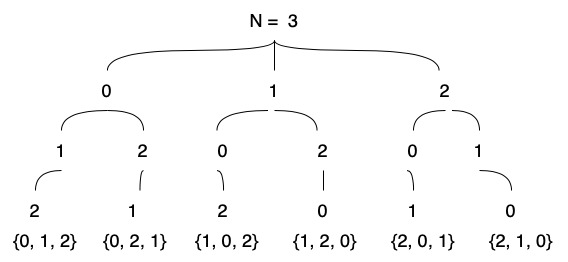
In order to generate every possible permutation we will use a recursive function, where we keep appending a unique number to the array until we have a complete permutation and then we go back and use a different number to get a different permutation. This is the tree that we build in order to achieve this, in this example N = 3.
static void generatePermutations(List <int[]>permList, LinkedHashSet<Integer> perm, int n){
if(perm.size() == n) {
permList.add(copyFromSet(perm));
return;
}
for(int i = 0; i < n; i++){
if(!perm.contains(i)) {
perm.add(i);
generatePermutations(permList, perm, n);
removeLastElement(perm);
}
}
}Now we gotta have some way to check if a permutation is a valid solution:
static boolean isSolution(int []perm){
for(int i = 0; i < perm.length - 1; i++) {
for(int j = i + 1; j < perm.length; j++){
if(Math.abs(i - j) == Math.abs(perm[i] - perm[j])){
return false;
}
}
}
return true;
}That piece of code checks if a queen is attacking another diagonally. Since we are using the index of the array to represent columns we know theres not gonna be more than one queen per column and the same applies for the rows since we are using 0 to N - 1 with no repetitions to represent the row where the queen is located, consider the following example:
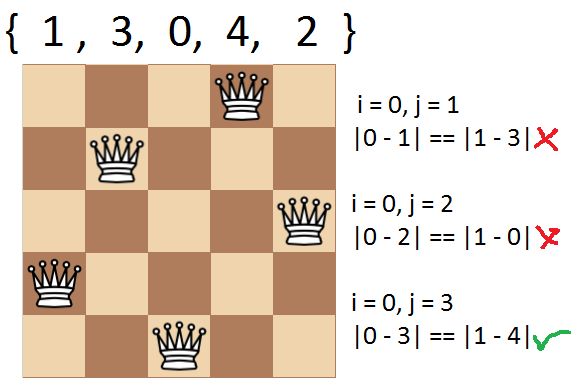
Since we got true for the if condition when i = 0 and j = 3 we know its not a valid solution.
Now we one have to put this together and we have our brute force approach for solving the N-Queens problem.
var permutations = new LinkedList<int[]>(); // permutations will be saved here
generatePermutations(permutations, new LinkedHashSet<Integer>(), n);
for(int []arr : permutations) {
if(isSolution(arr)) {
System.out.println(toString(arr)); // print valid solutions.
}
}The output of the program looks like this:
java NQueensBruteForce 6
{ 1 , 3 , 5 , 0 , 2 , 4 }
{ 2 , 5 , 1 , 4 , 0 , 3 }
{ 3 , 0 , 4 , 1 , 5 , 2 }
{ 4 , 2 , 0 , 5 , 3 , 1 }
Download the complete code from this post here NQueensBruteForce.java.